Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 혼자 공부하는 C언어
- Selection Sorting
- 알기쉬운 알고리즘
- 윤성우 열혈자료구조
- stream
- insertion sort
- 윤성우의 열혈 자료구조
- R
- coding test
- buffer
- list 컬렉션
- Stack
- JSON
- Algorithm
- 메모리구조
- s
- 이것이 자바다
- 이스케이프 문자
- C programming
- Serialization
- datastructure
- C 언어 코딩 도장
- Graph
Archives
- Today
- Total
Engineering Note
dijkstra 본문
dijkstra 최단경로 알고리즘
- 그래프에서 여러개의 노드가 있을 때, 특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단경로를 구해주는 알고리즘
- '음의 간선'이 없을 때 정상적으로 동작
- 현실세계에서의 길이 음의 간선으로 표현되지 않으므로 다익스트라 알고리즘은 실제로 GPX 소프트웨어의 기본 알고리즘을 채택되곤 한다.
- 현재 알고 있는 최단거리 정보를 가지고 최단거리표에 기록하고 그리디한 방법으로 최단거리이동 가능한 곳으로 이동해서 더 짧은 방법이 있으면 표를 갱신하는 방법이 핵심이다.
알고리즘의 원리
- 출발 노드를 설정한다. 출발노드까지의 거리는 0으로 초기화 한다.
- 최단 거리 테이블을 초기화한다.
- 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택한다.
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 위 과정에서 3과 4번을 반복한다.
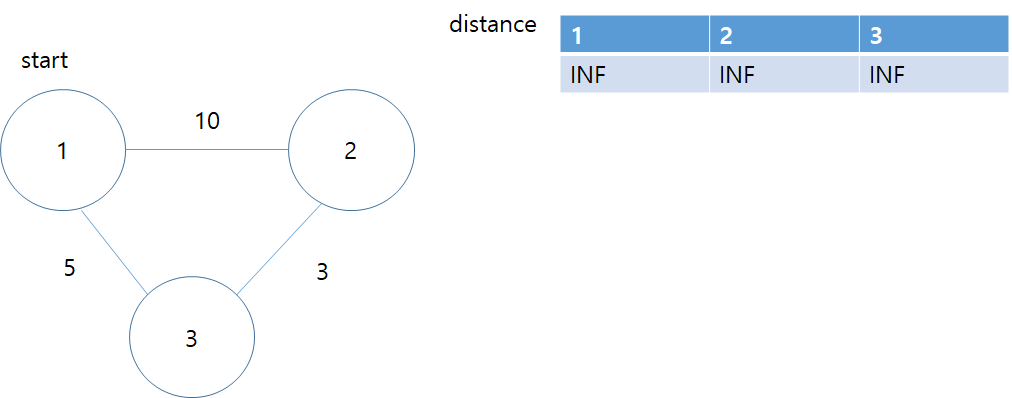
출발 노드 1을 선택하고 출발노드의 거리정보를 0으로 초기화 한다.
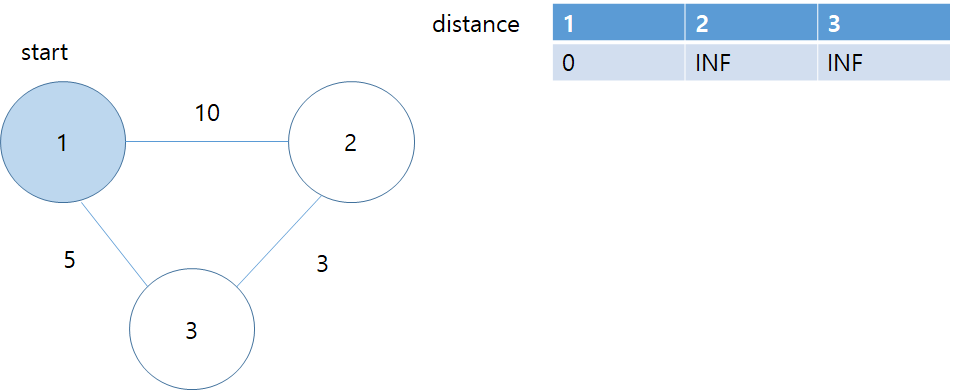
선택된 노드(1)를 거쳐 이동가능한 노드 정보를 기존 표와 비교해 최단 거리정보를 갱신한다. 1번 노드와 연결된 2번노드 3번노드까지의 이동거리는 10, 5이다. 10,5는 INF보다 짧으므로 갱신한다.

그 다음 표에서 방문하지 않은 가장 짧은 거리의 노드를 선택한다. 방금 방문한 1번을 제외하고 2,3번 노드 중에서 거리가 짧은 노드는 3번이므로 3번 노드를 선택한다.
3번을 거쳐 갈수 있는 2번 노드 까지의 거리는 3번까지 이동한 거리 5와 3번과 2번 사이의 거리 2를 더해 8(5+3)인데 기존 2까지 이동거리 10보다 짧으므로 갱신해준다.
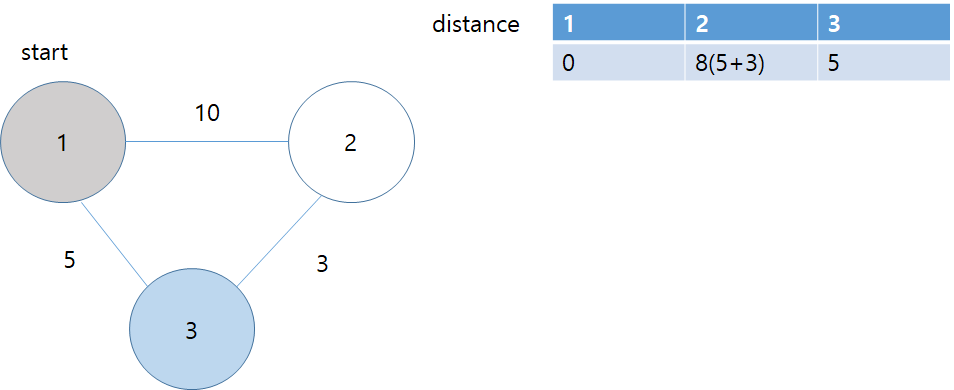
이제 방문하지 않고 가장 짧은 노드인 2번 노드를 선택하고 2번노드를 거쳐 이동 가능하고 방문하지 않은 노드가 없으므로 알고리즘을 종료한다.
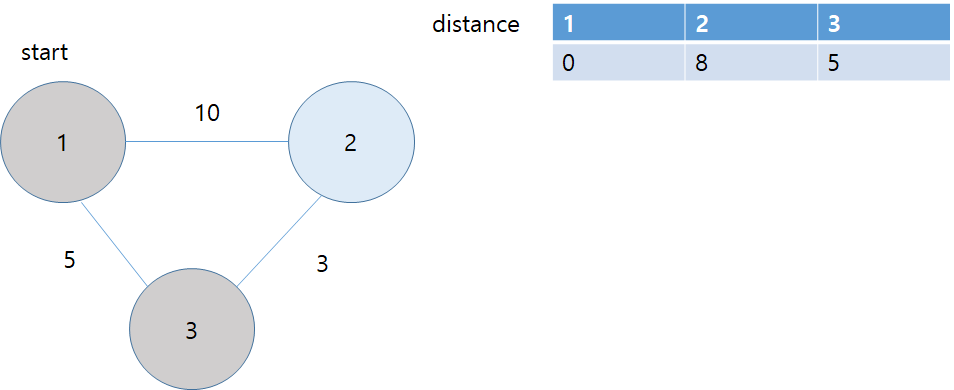
- 이렇게 최종 적으로 구해진 1번 노드부터 나머지 노드까지 이동가능한 최단 경로는 다음과 같다.

import sys
input = sys.stdin.readline
INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정
# 노드의 개수, 간선의 개수를 입력받기
n, m = map(int, input().split())
# 시작 노드 번호를 입력받기
start = int(input())
# 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n + 1)]
# 방문한 적이 있는지 체크하는 목적의 리스트를 만들기
visited = [False] * (n + 1)
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (n + 1)
# 모든 간선 정보를 입력받기
for _ in range(m):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b, c))
# 방문하지 않은 노드 중에서, 가장 최단 거리가 짧은 노드의 번호를 반환
def get_smallest_node():
min_value = INF
index = 0 # 가장 최단 거리가 짧은 노드(인덱스)
for i in range(1, n + 1):
if distance[i] < min_value and not visited[i]:
min_value = distance[i]
index = i
return index
def dijkstra(start):
# 시작 노드에 대해서 초기화
distance[start] = 0
visited[start] = True
for j in graph[start]:
distance[j[0]] = j[1]
# 시작 노드를 제외한 전체 n - 1개의 노드에 대해 반복
for i in range(n - 1):
# 현재 최단 거리가 가장 짧은 노드를 꺼내서, 방문 처리
now = get_smallest_node()
visited[now] = True
# 현재 노드와 연결된 다른 노드를 확인
for j in graph[now]:
cost = distance[now] + j[1]
# 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if cost < distance[j[0]]:
distance[j[0]] = cost
# 다익스트라 알고리즘을 수행
dijkstra(start)
# 모든 노드로 가기 위한 최단 거리를 출력
for i in range(1, n + 1):
# 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if distance[i] == INF:
print("INFINITY")
# 도달할 수 있는 경우 거리를 출력
else:
print(distance[i])'Computer Science > Data Structure & Algorithm' 카테고리의 다른 글
| [Data Structure] Binary Search Tree(BST) (0) | 2025.09.04 |
|---|---|
| Dynamic Programming (0) | 2022.05.26 |
| Priority Queue (0) | 2021.07.22 |
| 연결리스트 응용(주문 관리 시스템) (0) | 2021.07.07 |
| 유클리드 호재법 (0) | 2021.06.30 |
Comments

