Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- Algorithm
- JSON
- 메모리구조
- 이것이 자바다
- 혼자 공부하는 C언어
- Serialization
- C programming
- stream
- Graph
- s
- coding test
- 알기쉬운 알고리즘
- insertion sort
- 윤성우 열혈자료구조
- datastructure
- 윤성우의 열혈 자료구조
- buffer
- 이스케이프 문자
- Stack
- Selection Sorting
- list 컬렉션
- C 언어 코딩 도장
- R
Archives
- Today
- Total
Engineering Note
Graph 본문
Graph 정의
- '정점의 모음'과 이 정점을 잇는 '간선의 모음'과의 결합입니다. 즉 연결의 집합을 모형화 한것.
- 수학적인 표현으로는 "정접의 집합을 V, 간선의 집합을 E, 그리고 그래프를 G라고 했을 때 G = (V,E)이다."
- 정점 몇 개 자체로는 아무것도 아니지만 이들이 간선으로 인해 서로 연결될 때는 '관계'가 형성되고 이로 인해 그래프가 형성됩니다.
Graph의 중요성
- 위대한 수학자 오일러가 17세기에 개발한 이래, 그래프는 수많은 분야에서 도구로 사용되어 왔습니다.
- 서울 시청에서 버스노선을 정리할 때, 건축회사에서 시공 일정 계획을 할 때, 네이베기션이 경로를 탐색할 때 등 그래프의 응용 분야는 굉장히 다양합니다. 게다가 거의 모든 분야가 컴퓨터에 의존하고 있는 상황에서 프로그래머는 그래프를 반드시 이해해야 합니다.
Graph 표현방법의 생각 과정
- 그래프는 정점의 집합과 간선의 집합의 결합이기 때문에, 이를 표현하는 문제는 '정점의 집합'과 '간선의 집합'의 표현 문제로 생각할 수 있습니다.
- 정점의 잡합은 배열이나 링크드 리스트, 어떤 자료구조를 사용하더라도 쉽게 표현이 가능합니다. 문제는 간선의 집합을 표현하는 방법입니다. 이유는 간선은 그냥 선이 아니기 때문입니다. 간선은 정점과 정점이 '인접'관계에 있음을 나타내는 존재입니다.
- 즉, 그래프의 표현은 "간선, 즉 정점과 정점의 인접 관게를 어덯게 나타내는가?"의 문제로 귀결됩니다.
Graph의 표현 방법
- Graph를 나타내는 정점 사이의 인접관계를 나타내는 방법에는 크게 두 가지가 있습니다. 하나는 행렬을 이용하는 것이고, 또 다른 하나는 리스트를 이용하는 것입니다.
- 행렬을 이용하는 방식은 인접행렬(Adjacency Matrix)이라 하고 리스트를 이용하는 방식은 인접 리스트(Adjacency List)라고 부릅니다.
인접행렬 표현방법
- 그래프의 정점의 수를 N이라고 한다면, N*\N 크기의 행렬을 만들고 행렬의 각 원소를, 한 정점과 또 다른 정점이 인접해 있는 경우(즉, 점점사이에 간선이 존재하는 경우)에는 1로 표시하고, 인접해 있지 않은 경우에는 0으로 표시하는 것입니다.
인접리스트 표현 방법
- 각 정점에 대해 자신과 인접해 있는 모든 정점의 목록을 리스트로 관리하도록 하는 것입니다.
- 먼저 모든 정점을 죽 늘어놓고, 각 정점의 인접 정접을 옆에 나열합니다.
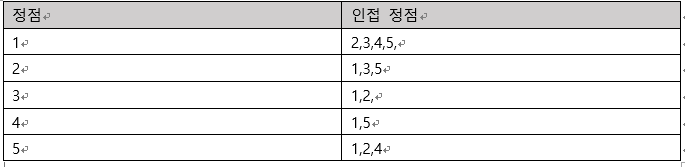
-------------------------------------------------------------------------------------------------------------
출처 : 뇌를 자극하는 알고리즘(한빛미디어, 박상현 저)
'Computer Science > Data Structure & Algorithm' 카테고리의 다른 글
| Dijkstra Algorithm (0) | 2021.04.15 |
|---|---|
| 최단경로 알고리즘 (0) | 2021.04.15 |
| Naver제출 소스코드 저장용 (0) | 2021.04.13 |
| 영지(territory) 선택 : (large) (0) | 2021.04.08 |
| 선택 정렬의 재귀적 구현 (0) | 2021.04.07 |
Comments


